
Magnetohydrodynamik (MHD)
Die MHD-Gruppe untersucht, entwickelt und analysiert robuste und effiziente Algorithmen für lineare und nichtlineare Magneto-Hydrodynamik, angewandt auf Tokamak- und Stellarator-Konfigurationen.
Die Gleichungen der Magnetohydrodynamik (MHD) können viele Aspekte der großskaligen Instabilitäten beschreiben, die in einem magnetisch eingeschlossenen Plasma auftreten.
Ein grundlegender Schritt bei der Modellierung eines Tokamaks oder Stellarators ist die Beschreibung des Zustands des eingeschlossenen Plasmas durch das sogenannte MHD-Gleichgewicht, bei dem die Kräfte des Magnetfelds mit dem Druckgradienten des Plasmas im Gleichgewicht stehen, und die Flächen mit konstantem Druck, sogenannte Flussflächen, ineinander verschachtelte Tori bilden.
Das MHD-Gleichgewicht ist eine nicht-triviale stationäre Lösung der idealen MHD-Gleichungen. Für die Berechnung solcher Gleichgewichte greift man auf dedizierte Löser zurück, die das Spulenfeld, Strom- und Druckprofile im Plasma berücksichtigen können.
Das MHD-Gleichgewicht ist der Ausgangspunkt für viele Simulationscodes. Es dient beispielsweise als Linearisierungszustand oder als Anfangszustand für zeitabhängige, nicht-lineare MHD-Simulationen. Die globale Lösung der nichtlinearen MHD-Gleichungen in der komplexen Geometrie eines Tokamaks oder Stellarators ist aufgrund der starken zeitlichen und räumlichen Mehrskaligkeit des Problems und des höchst anisotropen Verhaltens durch starke Magnetfelder eine sehr anspruchsvolle Aufgabe.
Die Forschungsthemen der MHD-Gruppe umfassen:
- 3D-MHD-Gleichgewichte: Entwicklung des Galerkin Variational Equilibrium Code (GVEC).
- Gittergenerierung: Die starke Anisotropie in MHD-Simulationen erfordert, dass die Gitter der Topologie des Magnetfeldes folgen müssen. Für realistische Simulationen von Tokamaks und Stellaratoren muss die Gittergenerierung das MHD-Gleichgewicht berücksichtigen oder sogar direkt mit einem Gleichgewichtslöser gekoppelt werden.
- Discontinuous-Galerkin-Verfahren (DG) hoher Ordnung: DG-Verfahren stellen die Lösung als Element-lokale Polynome dar und lösen Unstetigkeiten am Element-Interface durch eindeutige numerische Flüsse auf. Die Verfahren sind konservativ und hoher Ordnung. Aufgrund der Lokalität sind DG-Verfahren hoch skalierbar auf parallelen Computersystemen und daher gut geeignet für hoch aufgelöste Simulationen.
- Semi-implizite Zeitintegration: In magnetisch eingeschlossenen Plasmen ist die Zeitskala des MHD-Modells aufgrund starker Magnetfelder und niedriger Drücke durch die schnelle magnetosonische Welle stark eingeschränkt. Für Simulationen auf großer Zeitskala ist eine semi-implizite Behandlung vorteilhaft.
- In Zusammenarbeit mit der Gruppe strukturerhaltende Finite-Elemente-Methoden werden neue Diskretisierungen für lineare und nichtlineare MHD untersucht, die Struktureigenschaften, wie z.B. die Divergenzfreiheit des Magnetfelds, erhalten.
- In Zusammenarbeit mit der Gruppe kinetische und gyrokinetische Modelle werden die Stabilitätseigenschaften von strukturerhaltenden Diskretisierungen von Fluidmodellen untersucht, im Rahmen des Finite Element Exterior Calculus (FEEC).
3D-MHD-Gleichgewichtslöser

Abb. 1: Geometrie einer W7-X-Gleichgewichtslösung von GVEC
Während sich im Fall des Tokamaks das Gleichgewichtsproblem auf die Lösung einer nichtlinearen PDE, der zweidimensionalen Grad-Shafranov-Gleichung, reduziert, ist dies im dreidimensionalen Fall, wie bei Stelleratoren oder Tokamaks mit resonanten magnetischen Störungen, nicht möglich. Im dreidimensionalen Fall ist die Existenz von verschachtelten Flussflächen nicht garantiert, sie ist jedoch wichtig für einen guten Einschluss im Kern des Plasmas. Zum Beispiel minimiert der weit verbreitete Gleichgewichtscode VMEC die gesamte 3D-MHD Energie unter der Annahme geschlossener verschachtelter Flussflächen.
Unter Anwendung der gleichen Strategie wie in VMEC wurde am NMPP ein neuer 3D-MHD-Gleichgewichtscode GVEC (Galerkin Variational Equilibrium Code) von Grund auf neu entwickelt, sowie einer überarbeiteten theoretische Herleitung für den Minimierungsalgorithmus.
Ein Hauptunterschied zu VMEC ist die radiale Diskretisierung. Bei VMEC ist der radiale Gitterabstand equidistant im normierten Fluss. Dies führt zu einer höheren Auflösung am äußeren Rand und einer niedrigeren Auflösung an der Achse und wirkt sich auf die Genauigkeit der Gleichgewichtslösung aus. Im Vergleich dazu werden in GVEC B-Spline Finite Elemente mit nicht-equidistanten Gittern verwendet, was eine genaue Auflösung des gesamten radialen Bereichs einschließlich der magnetischen Achse ermöglicht und eine lokale Verfeinerung des Gitters erlaubt. Die B-Splines können von beliebigem Polynomgrad mit hoher Kontinuität sein, damit sind für eine bestimmte Genauigkeit weniger radiale Gitterpunkte erforderlich. Ausserdem wird eine glatte Darstellung radialer Ableitungen ermöglicht, die zur Auswertung von Gleichgewichtsgrößen (Metrik und Magnetfeld) benötigt werden. In Abb.1 ist die Geometrie einer W7-X-Gleichgewichtslösung visualisiert, mit lediglich 11 radiale Spline-Elemente von Polynomgrad 4.
Framework für nichtlineare MHD-Simulationen
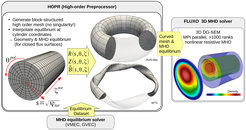
Das Simulationsframework ist in Abb.2 dargestellt. Als Vorbereitungsschritt erzeugt HOPR (high order preprocessor) ein gekrümmtes Gitter hoher Ordnung eines periodischen Zylinders, und unter Verwendung einer vorhandenen Gleichgewichtslösung aus VMEC oder GVEC wird der Zylinder auf die Flussflächengeometrie des Gleichgewichts abgebildet. Auch die Gleichgewichtsgrößen werden auf dem Gitter ausgewertet, und man somit Gitter und Anfangsbedingung für die nichtlineare MHD-Simulation in FLUXO erhält.
FLUXO ist ein open-source Projekt (project-fluxo), das in Zusammenarbeit mit dem Mathematischen Institut der Universität zu Köln entwickelt wird. FLUXO ist MPI-parallelisiert und die explizite Zeitintegration weist auf CPU-Architekturen eine exzellente schwache und starke Skalierung auf. Der Code löst allgemeine Advektions-Diffusionsgleichungen, wie z.B. Navier-Stokes-Gleichungen und die vollen resistiven MHD-Gleichungen, mit einer Discontinuous Galerkin-Spektralelement-Methode (DGSEM) auf unstrukturierten gekrümmten Hexaedergittern. FLUXO ermöglicht allgemeine split-form-Formulierungen der Gleichungen, und vor Kurzem wurde eine diskret entropiestabile split-form Formulierung implementiert.
Ausgewählte Publikationen:
Software:
- GVEC: 3D MHD Gleichgewichtscode, open-source release geplant, Zugang auf Anfrage.
- HOPR: Erstellung von 3D gekrümmten Gittern hoher Ordnung, mit Schnittstellen zu Gleichgewichtslösern.
- FLUXO: MPI paralleler 3D DGSEM Löser für allgemeine Advektions-Diffusionsgleichungen (Navier-Stokes, resistive MHD).

