MHD stability of stellarator plasma equilibria
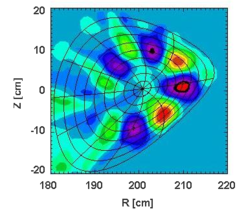
N=2 TAE in W7-AS discharge #39042 (soft-X-ray data)
In the framework of ideal MagnetoHydroDynamics (MHD), the fusion plasma is modelled as an ideally conducting fluid that is embedded in a confining magnetic field. Thus, Euler's and Maxwell's equations are the basis of ideal MHD. The linear stability properties, i.e., the response of a plasma equilibrium to small perturbations, can be cast into an energy principle for the ideal MHD force operator. Evaluating this energy principle, the spectrum of the force operator and the spatial structure of the perturbations can be determined. The method can be readily implemented for computational studies, and its applications are manifold. In the design of fusion devices, the knowledge thus obtained is useful for avoiding unstable configurations, where perturbations would grow exponentially with time. For experiments, the reconstruction and study of fluctuations (e.g. Alfven eigenmodes) in stable plasmas facilitate the understanding of experimentally obtained data.
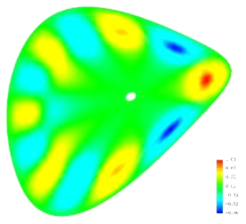
In a stellarator, the plasma does not possess a continuous symmetry, so that all stellaratory theory necessarily uses three independent space variables. This makes the theory more complicated than that in axisymmetric configurations. Although local stability criteria (Mercier, ballooning) are available, a full evaluation of stability requires a numerical approach. Of course, a general-geometry code can also be used for configurations with spatial symmetries, i.e. for axisymmetric (tokamak) and cylindrical plasma equilibria.
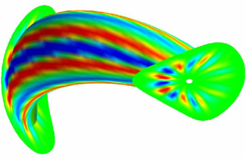
- Computational tools: VMEC 3D-MHD equilibrium code (S.P. Hirshman, ORNL);
CAS3D 3D-MHD stability code (C. Nuehrenberg, IPP). - methods: magnetic coordinates; energy principle; free-boundary perturbations;
solver for a vacuum region with an ideally conducting wall (P. Merkel, IPP);
Galerkin method (Fourier-FE); generalized algebraic eigenvalue problem;
block-multidiagonal matrices. - applications: determination of stability limits; study of stable spectra;
Alfven eigenmodes; perturbed equilibra (in collaboration with A. Boozer,
Columbia University, New York); wall stabilization of external perturbations. - further development: introduction of a kinetic-particle component (A. Koenies, IPP);
resistive wall-mode investigation (STARWALL code, P. Merkel, IPP).
reference:
C. Nuehrenberg, Phys. Plasmas 6, 137 (1999);
C. Nuehrenberg, Plasma Phys. Control. Fusion 41, 1055 (1999);
C. Nuehrenberg, Allen H. Boozer, and Stuart R. Hudson, Phys. Rev. Lett. 102, 235001 (2009). - for more information contact:
Carolin.Nuehrenberg[at]ipp.mpg.de


