MHD-Stabilität dreidimensionaler Plasmagleichgewichte
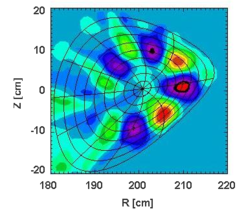
Hier wird das Plasmagleichgewicht im Rahmen der idealen Magnetohydrodynamik (Euler- und Maxwellgleichungen) modelliert und seine Reaktion auf kleine Störungen in ein Energieprinzip umgesetzt. Die Auswertung dieses Prinzips liefert das Spektrum des MHD-Kraftoperators mit den dazugehörigen räumlichen Störungen. Im Experimentdesign ist die Vermeidung von instabilen Plasmakonfigurationen mit zeitlich anwachsenden Störungen sehr wichtig. Während der Experimentierphase unterstützt die Untersuchung der Eigenschaften stabiler Schwingungen (z.B. TAEs, GAEs) die Dateninterpretation (z.B. an W7-AS, CHS).
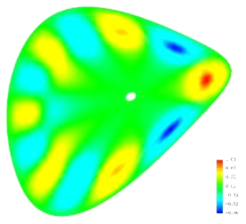
In Stellaratoren sind Plasmagleichgewichte inhärent dreidimensional, die sie betrachtende Theorie notwendigerweise ebenfalls. Deshalb wird hier das globale 3D-MHD-Stabilitätsproblem als solches betrachtet. Einerseits ist damit nur eine rechnergestützte Stabilitätsanalyse möglich, andererseits ersetzt diese die früher übliche Auswertung von lokalen Stabilitätskriterien (Mercier, Ballooning). Darüberhinaus kann der 3D-Code ebenfalls auf axialsymmetrische (2D) oder Zylinder- (1D) Plasmagleichgewichte angewendet werden.
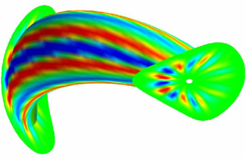
- Werkzeuge: VMEC 3D-MHD Gleichgewichtscode (S.P. Hirshman, ORNL); CAS3D 3D-MHD Stabilitätscode (C. Nührenberg, IPP).
- Methoden: magnetische Koordinaten; Energieprinzip; Störungen mit freien Randwerten; Vakuum mit Wand in endlicher Entfernung (P. Merkel, IPP); Galerkin-Verfahren (Fourier-FE); verallgemeinertes algebraisches Eigenwertproblem; blockmultidiagonale Matrizen.
- Anwendungsbereiche: Bestimmung von Stabilitätsgrenzen; Untersuchung stabiler Spektren; Alfvén Eigenmoden; Wandstabilisierung externer Moden.
- Fortführung: Einbeziehung des Einflusses kinetischer Teilchen (A. Könies, IPP).
- Referenz: C. Nührenberg, Phys. Plasmas 6, 137 (1999); C. Nührenberg, Plasma Phys. Control. Fusion 41, 1055 (1999).
- Informationen: Carolin.Nuehrenberg@ipp.mpg.de


