Geometric Numerical Integration and Reduced Complexity Modelling

The geometry group studies the abstract mathematical structures underlying plasma-physics models in order to design numerical algorithms that respect important qualitative properties of the physical problem.

Mathematical models in plasma physics are often extremely complex, reflecting the richness of plasma behaviour in nuclear fusion devices as well as in space and astrophysical plasmas. This is particularly true when such models are required to be physically realistic including full details on the geometry of the domain, boundary conditions and physics processes.

Despite the complexity of these models, which often consist of multiple coupled non-linear partial differential equations, they still reflect the fact that the systems they describe follow physical laws and possess certain symmetries and conservation laws. At a higher level of mathematical abstraction, this is referred to as the mathematical structure of the model, which can often be understood in terms of modern Geometric Mechanics. By means of geometric or structure-preserving methods, such mathematical structures are exploited in order to obtain qualitatively better numerical solutions that respect the physical conservation laws, devise new efficient algorithms for problems that are either not amenable to or extremely slow with standard discretization techniques, and suggest better formulations of reduced models that respect the structure of the original model.

Geometric and Structure-preserving Numerical Algorithms

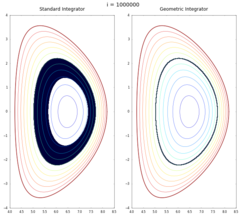
Many conservative systems in physics feature a Hamiltonian or Lagrangian structure, that is their dynamics can be described in terms of a bilinear operator, called Poisson bracket, and an energy functional, called the Hamiltonian, or in terms of an action principle. This is the case, for example, for ideal magnetohydrodynamics and the Vlasov-Maxwell system.
Preserving the Hamiltonian or Lagrangian structure at the discrete level leads to numerical methods which satisfy important conservation laws, either exactly or within tight error bounds, and reproduce the qualitative correct physical behaviour also in long-time and strongly nonlinear simulations.

The application of geometric integration techniques such as symplectic or variational integrators to charged particle dynamics (ordinary differential equations) or plasma field theories (partial differential equations) is usually not readily possible due to the noncanonical nature of plasma physics models. The geometry group develops appropriate extensions of geometric numerical integration methods, that are required in order to deal with important plasma physics models such as guiding centre dynamics, magnetohydrodynamics and kinetic physics.

In order to include certain non-ideal effects, such as collisions in kinetic models, the ideal formulations can be extended: the Hamiltonian formulation by a metric bracket and an entropy functional that is dissipated, leading to the so-called metriplectic framework; and the Lagrangian formulation by the inclusion of forcing terms, leading to the Lagrange-d'Alembert framework. These formulations, even though non-ideal, feature rich geometric structures, including conservation laws or so-called Dirac structures, that are sought to be preserved in computer simulations in order to describe the underlying physics correctly, in particular the laws of thermodynamics.

Reduced Complexity Modelling

Reduced complexity modelling aims to capture the behaviour of a complex system while at the same time saving computational cost. For parameter-dependent systems, reduced order models can be developed using the results of sample 'training' simulations using select parameter values to then simulate the system for numerous other parameters using a cheaper reduced model. This is very beneficial in multi-query applications, where the reduced model has to be evaluated many times, for example inside an optimization loop or the solution of an inverse problem.

Other approaches like low-rank approximation techniques aim at finding compressed representations of a system that allow for an accurate description of its dynamics while requiring dramatically reduced numbers of degrees of freedom than standard numerical methods. These methods do not require a training phase and thus have the potential to be applicable over larger parameter ranges and in situations where collecting a sufficiently large number of training data is not computationally feasible.

Our focus is on the development of new reduced complexity models that preserve important mathematical structures of the high-fidelity models in the reduction process. This allows us to construct reduced models which require even lower numbers of degrees-of-freedom than standard complexity reduction techniques while at the same time representing the underlying physics more accurately.

Scientific Machine Learning

Scientific machine learning is an emerging research area that uses machine learning techniques to address problems across all sciences. In plasma physics, hybrid approaches where physics-based methods are combined with data-driven methods e.g. to solve differential equations (physics informed machine learning) are particularly promising.

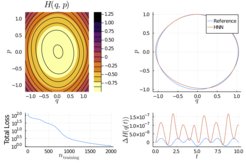
The geometry group studies the design of neural network architectures, that encode important properties of the equations being solved. Geometry guides the design process to facilitate networks that are specifically tailored to the solution of a specific problem.
By this approach it is even possible to construct training-free neural networks for the structure-preserving solution of differential equations, where for a given problem the network can be completely pre-computed.

Selected Publications

Software

• GeometricIntegrators.jl
  Bibliothek geometrischer Integratoren für gewöhnliche Differentialgleichungen und Differential-algebraische Gleichungen in Julia.
• GeometricMachineLearning.jl
  Structure-preserving machine learning models
• ReducedBasisMethods.jl
  Structure-preserving reduced basis methods