Geometrische numerische Integration und Modellierung reduzierter Komplexität

Die Geometriegruppe nutzt die abstrakten mathematischen Strukturen, die den Modellen der Plasmaphysik zugrunde liegen, um numerische Algorithmen zu entwerfen, die qualitative Eigenschaften der physikalischen Systeme erhalten.

Das Verhalten sowohl von Fusions- als auch von astrophysikalischen Plasmen ist von einer Vielzahl physikalischer Phänomene geprägt und durch deren Zusammenspiel hochgradig kompliziert. Dies spiegelt sich in den mathematischen Modellen der Plasmaphysik wieder, die oft äußerst komplex sind, insbesondere wenn die Modelle physikalisch realistisch sein sollen und alle Details der Geometrie, der Randbedingungen und der physikalischen Prozesse berücksichtigen sollen.

Auf einer höheren Ebene mathematischer Abstraktion zeigen solche komplizierten Modelle häufig eine reichhaltige und elegante "Struktur", die oft in Begriffen der modernen geometrischen Mechanik verstanden werden können. Strukturerhaltende Methoden nutzen solche mathematischen Strukturen aus, um qualitativ besserer numerische Lösungen zu erhalten, die physikalische Erhaltungssätze bewahren. Die Geometriegruppe entwickelt neue effiziente Algorithmen für Probleme, die mit Standardverfahren nicht oder nur extrem langsam lösbar sind, sowie bessere Formulierungen reduzierter Modelle, die die Struktur der ursprünglichen Modelle erhalten.

Geometrische numerische Integration

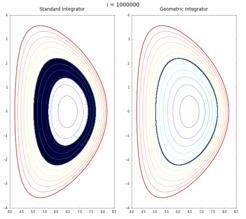
Viele konservative Gleichungssysteme der Physik haben eine Hamilton'sche oder Lagrange'sche Struktur. Im ersten Fall wird die Dynamik mittels eines bilinearen Operators, der sogenannten Poisson-Klammer, und eines Energiefunktionals, der sogenannten Hamilton-Funktion, beschrieben. Im zweiten Fall folgen die Gleichungen aus einem Wirkungsprinzip. Dies ist beispielsweise bei der idealen Magnetohydrodynamik und dem Vlasov-Maxwell-System der Fall.
Die Erhaltung der Hamilton'schen oder Lagrange'schen Struktur auf der diskreten Ebene führt zu numerischen Verfahren, die wichtige Erhaltungssätze entweder exakt erhalten oder innerhalb enger Fehlerschranken, und das physikalische Verhalten qualitativ korrekt reproduzieren, insbesondere in Langzeit- und stark nichtlinearen Simulationen.

Die Anwendung geometrischer Integrationsverfahren wie symplektische Methoden oder Variationsintegratoren auf die Dynamik geladener Teilchen (gewöhnliche Differentialgleichungen) oder plasmaphysikalische Feldtheorien (partielle Differentialgleichungen) ist meist nicht ohne weiteres möglich, da diese Modelle üblicherweise nichtkanonische geometrische Strukturen aufweisen.
Die Geometriegruppe entwickelt geometrische Integrationsverfahren, die auch auf Gleichungssysteme mit solch komplizierten Strukturen angewandt werden können, was nötig ist um Modelle der Plasmaphysik wie zum Beispiel  Guiding Center Dynamik, Magnetohydrodynamik oder kinetische Modelle behandeln zu können.

Um bestimmte nicht-ideale Effekte wie beispielsweise Stöße in kinetischen Modellen zu berücksichtigen, müssen die idealen Modelle erweitert werden: die Hamilton'sche Formulierung durch eine metrische Klammer und ein Entropiefunktional, das dissipiert wird, was zur sogenannten metriplektischen Formulierung führt; die Lagrange'sche Formulierung wird um bestimmte Kraftausdrücke erweitert, was zur Lagrange-d'Alembert-Formlierung führt.
Obgleich diese Formulierungen nicht ideal sind, weisen sie reichhaltige geometrische Strukturen auf, beispielsweise Erhaltungssätze oder sogenannte Dirac-Strukturen, die in Computersimulationen möglichst erhalten bleiben sollten, damit die zugrundeliegende Physik, insbesondere die Gesetze der Thermodynamik, korrekt beschrieben wird.

Reduced Complexity Modelling

Reduced Complexity Modelling bezeichnet die Konstruktion vereinfachter Systeme, die das Verhalten komplexer Systeme korrekt abbilden aber geringere Rechenzeit benötigen. Für parameterabhängige Systeme können Modelle reduzierter Ordnung konstruiert werden, die aus den Ergebnissen einer Zahl von Traniningssimulationen für bestimmte Parameterwerte konstruiert werden, um kostengünstige Simulationen für eine Vielzahl anderer Parameter auszuführen. Dieser Ansatz ist insbesondere in many-query Anwendungen, in denen das reduzierte Modell viele male ausgewertet werden muss, vorteilhaft, beispielsweise in Optimierungsalgorithmen oder bei der Lösung inverser Probleme.

Andere Ansätze wie Niedrig-Rang-Approximationen versuchen komprimierte Darstellungen eines Systems zu finden, die eine viel geringere Anzahl von Freiheitsgraden als herkömmliche numerische Verfahren benötigen, aber dennoch in der Lage sind, die Dynamik des Systems genau zu beschreiben. Diese Verfahren benötigen kein Training und sind daher potentiell auf größere Parameterbereiche anwendbar sowie auf Probleme, für die die Berechnung einer hinreichen großen Anzahl von Trainingsdatensätzen nicht möglich ist.

Unser Schwerpunkt ist die Entwicklung von Modellen reduzierter Komplexität, die wichtige mathematische Strukturen der ursprünglichen Modelle erhalten. Dies erlaubt die Konstruktion reduzierter Modelle, die noch weniger Freiheitsgrade benötigen als herkömmliche Modellreduktionsverfahren und trotzdem die zugrunde liegende Physik besser reproduzieren.

Scientific Machine Learning

Scientific Machine Learning ist ein wachsender Forschungszweig, der Techniken des maschinellen Lernens benutzt, um verschiedene Probleme aus den Naturwissenschaften zu lösen. In der Plasmaphysik sind insbesondere hybride Ansätze interessant, bei denen physikbasierte Verfahren mit datengetriebenen Verfahren kombiniert werden, beispielsweise um Differentialgleichungen zu lösen (Physics Informed Machine Learning).

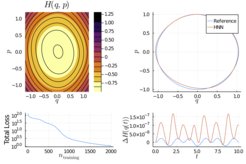
Die Geometriegruppe befasst sich mit der Konstruktion neuartiger Architekturen von neuronalen Netzwerken, die wichtige Eigenschaften der Gleichungen, die gelöst werden sollen, enkodieren, beispielsweise ihre Hamilton'sche oder Lagrange'sche Struktur. Die zugrundeliegende Geometrie leitet dabei den Designprozess und ermöglicht Netzwerkarchitekturen, die auf die Lösung eines spezifischen Problems hin optimiert sind.
Dieser Ansatz erlaubt sogar die Konstruktion trainingsloser neuronaler Netzwerke für die strukturerhaltende Lösung von Differentialgleichungen, bei der sämtliche Parameter des Netzwerkes für ein gegebenes Problem berechnet werden können.

Ausgewählte Publikationen

Software

• GeometricIntegrators.jl
  Bibliothek geometrischer Integratoren für gewöhnliche Differentialgleichungen und Differential-algebraische Gleichungen in Julia.
• GeometricMachineLearning.jl
  Structure-preserving machine learning models
• ReducedBasisMethods.jl
  Structure-preserving reduced basis methods