Magnetohydrodynamics

The MHD group of the NMPP division works on the study, development and analysis of robust and efficient algorithms for linear and nonlinear magneto-hydrodynamics, applied to tokamak and stellarator configurations.

The magneto-hydrodynamics (MHD) equations can describe many aspects of large-scale instabilities that appear in a magnetic confined plasma.
A basic step in the modelling of a tokamak and a stellarator is to describe the confined plasma state by a so-called MHD equilibrium, where the magnetic field forces balance the pressure gradient of the plasma, and where the contours of constant pressure form a set of nested tori or flux surfaces.
The MHD equilibrium is a non-trivial steady state solution of the ideal MHD equations. For the computation of such equilibria, one resorts to dedicated solvers which can take into account the coil field, current and pressure profiles inside the plasma.
The MHD equilibrium is the starting point for many simulation codes. It can be used as a linearization state or as an intial state for time-dependent non-linear MHD simulations.
Solving the nonlinear MHD equations globally in the complex geometry of a tokamak or a stellarator is a highly demanding task due to the strong temporal and spatial multi-scale nature of the problem and highly anisotropic behaviour arising from strong magnetic fields.

The research topics of the MHD group include:

• 3D MHD equilibria: development of the Galerkin Variational Equilibrium Code (GVEC).
• Mesh Generation: The strong anisotropy in MHD simulations requires that meshes must follow the topology of the magnetic field. In order to achieve realistic simulations in both tokamaks and stellarators, meshes have to be generated with the knowledge of an MHD equilibrium or even by coupling to an equilibrium solver.
• High Order Discontinuous Galerkin Method: DG methods represent the solution by element-local polynomials and discontinuities at element interfaces are resolved via unique numerical fluxes. The scheme is conservative and high order. Due to its locality, DG is highly scalable and therefore well suited for large-scale parallel computations.
• Semi-implicit time integration: In magnetic confined plasma, due to strong magnetic fields and low pressures, the time scale of the MHD model is severely constraint by the fast magnetosonic wave. For large timescale simulations, an semi-implicit treatment is favorable.
• Together with the group of Structure-Preserving Finite Element Methods, new discretizations for linear and nonlinear MHD that preserve structures such as divergence-free magnetic fields are investigated.
• Together with the group of Kinetic and gyrokinetic models, we study stability properties of structure-preserving discretizations of fluid-type models in the framework of finite element exterior calculus (FEEC).

3D MHD equilibrium solver

While in the  tokamak case, the equilibrium problem reduces to solving a non-linear PDE, the two-dimensional Grad-Shafranov equation, this is not possible in the three-dimensional case, such as stellerators or tokamaks with resonant magnetic perturbations. In 3D, the existence of nested flux surfaces is not guaranteed, however, it is important for good confinement in the plasma core. For example, the well-established equilibrium code VMEC minimizes total 3D MHD energy under the assumption of closed nested flux surfaces.  

Adopting the same strategy as VMEC, a new 3D MHD equilibrium code GVEC (Galerkin Variational Equilibrium Code)  was developed from scratch at NMPP, also revisiting thoroughly the theoretical derivations for the minimization algorithm.
A main difference to VMEC is the radial discretisation. In VMEC, the radial grid spacing is uniform in the normalised flux, which leads to a higher resolution at the outer boundary and a lower resolution at the axis, affecting the accuracy of the equilibrium solution. In comparison, in GVEC, B-Spline Finite Elements with a non-uniform grid spacing are used, allowing to accurately resolve the full radial domain including the magnetic axis and allowing local refinement of the grid. The B-Splines can be of arbitrary polynomial degree with a high continuity, which means that less radial grid points are needed for a certain accuracy. In addition, they allow to smoothly represent radial derivatives, needed to evaluate equilibrium quantities such as metrics and magnetic field. In Fig.1, the geometry of a W7-X equilibrium solution is shown, using only 11 radial spline elements of polynomial degree 4.
  

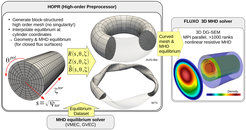
Nonlinear MHD simulation framework

The simulation framework is depicted in Fig.2. As a preprocessing step, HOPR (high order preprocessor) generates a curved high order mesh of a periodic cylinder,
and using an existing equilibrium solution from VMEC or GVEC, the cylinder is mapped to the flux surface geometry of the equilibrium. Also the equilibrium quantities are evaluated on the mesh,
serving as the mesh and initial condition for the nonlinear MHD simulation in FLUXO.

FLUXO is an open-source project (project-fluxo) developed in collaboration with the Mathematical Institute at the University of Cologne.  
FLUXO is MPI parallelized and the explicit time integration exhibits excellent weak and strong scaling on current CPU architectures.
The code solves general advection-diffusion equations, such as Navier-Stokes equations and the full resistive MHD equations, with a Discontinuous Galerkin Spectral Element Method (DGSEM) on unstructured curvilinear hexahedral meshes.
FLUXO allows for general split-form formulations of the equations, and a discretely entropy stable split-form has been recently implemented.

Selected Publications:

Software:

• GVEC: 3D MHD equilibrium code, to be released open-source, access granted on demand.
• HOPR: 3D Mesh generation of high order curved meshes, with interfaces to equilibrium solvers.
• FLUXO: MPI parallel 3D DGSEM solver for general advection-diffusion equations (Navier-Stokes, resistive MHD).